What is Thermal Stress in Strength of Materials?

In this article we will learn about what is thermal stress and formula of thermal stress and strain.

What is Thermal Stress?

Stress which is induced in a body due to change in the temperature is known as thermal stress and the corresponding strain is called thermal strain.

Thermal stress induces in a body when the temperature of the body is raised or lowered and the body is not allowed to expand or contract freely. No stress will be induced in a body when it is allowed to expand
or contract freely.

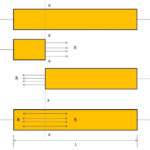
Considered a body (for example a rod) which is heated to a specified temperature?

Let

L = Original length of the rod,

T = Rise in temperature,

E = Young’s modulus,

α = Coefficient of linear expansion and

dL = Extension produced in the rod

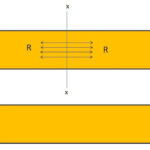
Due to the increase in the temperature, there is an extension produced in the rod. When the rod is allowed to expand freely, the extension produced in the rod is given by

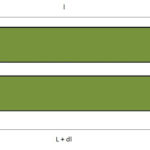
This is shown in the diagram given above, here AB is the original length of the rod, and BB’ is the extension produced in the rod. Suppose a compressive load P is applied at the end BB’, Due to this
compressive load, there is a decrease in the length of the rod from (L + dL) to L. Compressive stress and strain is produced in the rod and is given by

Thrust or load on the rod is given by

When the ends of the rod is rigidly fixed with the supports and the rod is heated to a certain temperature, here the extension in the rod is prevented because we have rigidly fixed it’s both the
ends. Stress and strain is setup in the rod. The stresses and strain setup in the rod is known as thermal stresses and strains.

Thermal strain is given by

Thermal stress-induced is given by

Stress and Strain When the Supports Yield

If the supports at the ends yield by an amount equal to the δ, then

This is all about what is thermal Stress in the strength of materials. If you found this piece of information valuable and useful then don’t forget to like and share it.